Kvantummechanikai bevezető példák - Emissziós spektrum korrekciója visszalökődéssel

Feladat

1. Határozza meg, hogy az atomok fotonkibocsátásakor fellépő visszalökődés milyen korrekciót jelent az emissziós spektrumban!

Megoldás

Oldjuk meg a feladatot arra a két esetre, amikor a kibocsátott foton az atommag kezdeti sebességével azonos, illetve ellentétes irányú, így kapjuk az emissziós spektrumban a legnagyobb eltolódásokat. Az energiamegmaradás $\setbox0\hbox{$1$}% \message{//depth:\the\dp0//}% \box0%$-gyel a kezdő, $\setbox0\hbox{$2$}% \message{//depth:\the\dp0//}% \box0%$-vel a végállapotot indexelve:

$\[ E_1 + \frac12 Mv_1^2 = E_2 + \frac12 M v_2^2 + h\nu', \]$

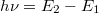ahol $\setbox0\hbox{$h\nu = E_2-E_1$}% \message{//depth:\the\dp0//}% \box0%$ a korrekció nélkül kapott foton energiája, hasonló módon felírjuk az impulzusmegmaradást a két esetre:

$\[ M v_1 = M v_2 \pm \frac{h\nu'}{c}. \]$

Az energiamegmaradásból fejezzük ki a korrigált és az „eredeti” foton energiájának különbségét:

$\[ h(\nu-\nu') = \pm \frac12 M(v_1-v_2)(v_1+v_2) = \pm \frac12 \frac{h\nu'}{c}(v_1+v_2), \]$

ahol az utolsó lépésben az impulzusmegmaradást használtuk. Ismét az impulzusmegmaradásból

$\[ v_2=v_1\mp\frac{h\nu'}{Mc}, \]$

amivel

$\[ h(\nu-\nu') = \pm \frac12 M(v_1-v_2)(v_1+v_2) = \pm \left(\frac{h\nu'}{c}v_1 - \frac{(h\nu')^2}{Mc^2} \right). \]$

Itt két effektus figyelhető meg:

• a fotont kibocsátó atom sebessége nagy (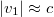$\setbox0\hbox{$|v_1|\approx c$}% \message{//depth:\the\dp0//}% \box0%$) vagy az atomot rögzített nem tekintjük (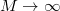$\setbox0\hbox{$M\to\infty$}% \message{//depth:\the\dp0//}% \box0%$), akkor a frekvencia a Doppler-effektusnak megfelelően tolódik el
• az álló atom által (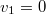$\setbox0\hbox{$v_1=0$}% \message{//depth:\the\dp0//}% \box0%$) kibocsátott foton energiája kisebb, mint a rögzített atomra végzett számításból adódna: az átmenet energiájának egy részét az atommag viszi el kinetikus energia formájában. A számításból adódik, hogy foton elnyelésénél pedig nagyobb energiákra van szükség, mint amit a kibocsátott fotonok hordoznak, ez mérhető és felfedezőjéről Mössbauer-effektusnak nevezzük.