Kvantummechanikai bevezető példák - Fekete test fotonáramsűrűsége
A Fizipedia wikiből
| [rejt] Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Kvantummechanikai bevezető |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Határozzuk meg, hogy egy
 hőmérséklet fekete test milyen foton-áramsűrűséggel sugároz!
hőmérséklet fekete test milyen foton-áramsűrűséggel sugároz!
Megoldás
A Planck-féle sugárzási törvény szerint a fekete test által a teljes térszögbe a ![\setbox0\hbox{$[\nu, \nu+\mathrm{d}\nu]$}% \message{//depth:\the\dp0//}% \box0%](/images/math/f/c/9/fc93547493d2a6e8d98d5ee5959083a9.png) frekvenciaintervallumban felületegységenként kisugárzott teljesítményt átírjuk, hogy megjelenjen a foton
frekvenciaintervallumban felületegységenként kisugárzott teljesítményt átírjuk, hogy megjelenjen a foton 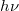 energiája:
energiája:
![\[ \mathcal{E}_\nu\,\mathrm{d}\nu = \frac{8\pi}{c^2} \frac{h\nu^3}{e^{\textstyle \frac{h\nu}{kT}}-1}\,\mathrm{d}\nu = h\nu \cdot \frac{8\pi}{c^2} \frac{\nu^2}{e^{\textstyle \frac{h\nu}{kT}}-1}\,\mathrm{d}\nu, \]](/images/math/a/c/0/ac0ffb38ed4f2df712a5571ce9ff5de2.png)
ami alapján bevezetjük a teljes térszögbe a ![\setbox0\hbox{$[\nu, \nu+\mathrm{d}\nu]$}% \message{//depth:\the\dp0//}% \box0%](/images/math/f/c/9/fc93547493d2a6e8d98d5ee5959083a9.png) frekvenciaintervallumban felületegységenként kisugárzott fotonszámot:
frekvenciaintervallumban felületegységenként kisugárzott fotonszámot:
![\[ n(\nu)\,\mathrm{d}\nu = \frac{8\pi}{c^2} \frac{\nu^2}{e^{\textstyle \frac{h\nu}{kT}}-1}\,\mathrm{d}\nu. \]](/images/math/b/c/0/bc069d42596b7ba4852bedc10e5989aa.png)
A fotonok teljes száma felületegységenként és időegységenként 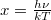 változócserével:
változócserével:
![\[ N = \int_0^\infty n(\nu)\,\mathrm{d}\nu = \frac{8\pi}{c^2}\left(\frac{kT}{h}\right)^3 \int_0^\infty \frac{x^2}{e^x-1}\,\mathrm{d}x, \]](/images/math/e/7/e/e7e49779ae5f36a6e684a8733896d57d.png)
ahol az integrál kifejezhető a Riemann-féle 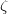 -függvénnyel, értéke
-függvénnyel, értéke 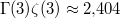 .
.
Például 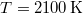 -en
-en
![\[ N = 5{,}64\cdot 10^{25}\,\mathrm{\frac{1}{s\,m^2}}, \]](/images/math/e/a/1/ea13424bf117dd39c6fcb68e73a6e3ca.png)
amit értelmezhetünk 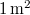 -en
-en 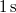 alatt létrejövő
alatt létrejövő 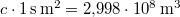 térfogatban egyenletesen eloszló kb.
térfogatban egyenletesen eloszló kb. 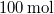 fotonként.
fotonként.