„Kvantummechanikai bevezető példák - Bohr-féle hidrogénmodell kéttest korrekciója” változatai közötti eltérés

A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika 3. gyakorlat Kategória:Szerkesztő:Stippinger Kategória:Kvantummechanikai bevezető {{Kísérleti fizika gyakorlat …”)
 
9. sor: 9. sor:
 
}}
 
}}
 
== Feladat ==
 
== Feladat ==
−
</noinclude><wlatex># Számítsa ki, hogy a hidrogénatom Bohr-féle modelljében a mag véges nagyságú tömege milyen korrekciót jelentene az energiaszintekben és a spektrumban!</wlatex><includeonly><wlatex>{{Útmutatás|content=$$keplet$$}}{{Végeredmény|content=$$keplet$$}}</wlatex></includeonly><noinclude>
+
</noinclude><wlatex># Számítsa ki, hogy a hidrogénatom Bohr-féle modelljében a mag véges nagyságú tömege milyen korrekciót jelentene az energiaszintekben és a spektrumban!</wlatex><includeonly><wlatex>{{Útmutatás|content=Oldja meg a Bohr-modellt tömegközépponti koordináta-rendszerben.}}{{Végeredmény|content=$$E_n^* = -\frac{E_0}{n^2},$$ $$ E_0^* = \frac{E_0}{1+\textstyle \frac{m_e}{M}} \approx E_0 \left(1- \frac{m_e}{M}\right), $$ ahol $m_e$ az elektron, $M$ pedig az atommag tömege.}}</wlatex></includeonly><noinclude>
 
== Megoldás ==
 
== Megoldás ==
−
<wlatex>Megoldás szövege
+
<wlatex>A kéttest korrekciónál a [[Kvantummechanikai bevezető példák - Bohr-féle hidrogénmodell|Bohr-modell]] tárgyalásából továbbra is érvényes, hogy a Coulomb-erő tölti be a centipetális erő szerepét
 +
$$ m_e \frac{v^2}{r} \equiv m_e \omega^2 r = \frac{1}{4\pi\varepsilon_0}\frac{e^2}{r^2}, $$
 +
de az impulzusmomentum kvantálását most az atommag és az elektron összes impulzusmomentumára alkalmazzuk:
 +
$$ m_e r_e^2 \omega + M r_M^2 \omega = n\hbar, $$
 +
ahol $M$ az atommag tömege, $r_e$ és $r_M$ rendre az elektron és az atommag pályasugara a közös tömegközéppont körül, $\omega$ pedig a közös keringési körfrekvencia.
 +
 
 +
A tömegközéppont definíciójából
 +
$$ r_e = \frac{M}{m_e + M}, \qquad  r_M = \frac{m_e}{m_e + M}, $$
 +
ahol $r$ az elektron és az atommag távolsága. Bevezetjük még a
 +
$$ \mu = \frac{m_e M}{m_e + M} $$
 +
redukált tömeget. Ezekkel a két egyenletünk:
 +
$$ \mu r_n \omega_n^2 = \frac{1}{4\pi\varepsilon_0}\frac{e^2}{r_n^2}, $$
 +
$$ \mu r_n^2 \omega_n = n\hbar, $$
 +
ami a [[Kvantummechanikai bevezető példák - Bohr-féle hidrogénmodell|Bohr-modellével]] megegyező egyenletrendszer, a kéttest korrekcióval javított energiaszintek a korábbi $E_n^* = -\frac{E_0}{n^2}$ módon számolhatók az új
 +
$$ E_0^* = E_0 \frac{\mu}{m} = \frac{E_0}{1+\textstyle \frac{m_e}{M}} \approx E_0 \left(1- \frac{m_e}{M}\right) $$
 +
ionizációs energiával,
 +
ahol $\frac{m_e}{M}\approx\frac{1}{1835}$.
 +
 
 
</wlatex>
 
</wlatex>
 
</noinclude>
 
</noinclude>

A lap 2013. április 23., 20:01-kori változata

Navigáció Pt·1·2·3
Kísérleti fizika 3. gyakorlat
Gyakorlatok listája:
  1. Kinetikus gázelmélet, transzport
  2. Állapotváltozás, I. főtétel
  3. Fajhő, Körfolyamatok
  4. Entrópia, II. főtétel
  5. Homogén rendszerek
  6. Fázisátalakulások
  7. Kvantummechanikai bevezető
Kvantummechanikai bevezető
Feladatok listája:
  1. Nap felszíni hőmérséklete
  2. Izzólámpa hatásfoka
  3. Fekete test
  4. Tantál kilépési munkája
  5. Compton-szórás
  6. Compton-szórás szabadon
  7. Fluxuskvantálás
  8. Bohr-modell
  9. Rel. tömegnövekedés
  10. Kéttest korrekció
  11. Visszalökődés
  12. Korrespondencia-elv
  13. Foton és elektron Ekin(k)
  14. Schrödinger-egyenlet
© 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064

Feladat

  1. Számítsa ki, hogy a hidrogénatom Bohr-féle modelljében a mag véges nagyságú tömege milyen korrekciót jelentene az energiaszintekben és a spektrumban!

Megoldás

A kéttest korrekciónál a Bohr-modell tárgyalásából továbbra is érvényes, hogy a Coulomb-erő tölti be a centipetális erő szerepét

\[ m_e \frac{v^2}{r} \equiv m_e \omega^2 r = \frac{1}{4\pi\varepsilon_0}\frac{e^2}{r^2}, \]

de az impulzusmomentum kvantálását most az atommag és az elektron összes impulzusmomentumára alkalmazzuk:

\[ m_e r_e^2 \omega + M r_M^2 \omega = n\hbar, \]

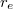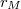ahol \setbox0\hbox{$M$}% \message{//depth:\the\dp0//}% \box0% az atommag tömege, \setbox0\hbox{$r_e$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$r_M$}% \message{//depth:\the\dp0//}% \box0% rendre az elektron és az atommag pályasugara a közös tömegközéppont körül, \setbox0\hbox{$\omega$}% \message{//depth:\the\dp0//}% \box0% pedig a közös keringési körfrekvencia.

A tömegközéppont definíciójából

\[ r_e = \frac{M}{m_e + M}, \qquad r_M = \frac{m_e}{m_e + M}, \]

ahol \setbox0\hbox{$r$}% \message{//depth:\the\dp0//}% \box0% az elektron és az atommag távolsága. Bevezetjük még a

\[ \mu = \frac{m_e M}{m_e + M} \]

redukált tömeget. Ezekkel a két egyenletünk:

\[ \mu r_n \omega_n^2 = \frac{1}{4\pi\varepsilon_0}\frac{e^2}{r_n^2}, \]
\[ \mu r_n^2 \omega_n = n\hbar, \]

ami a Bohr-modellével megegyező egyenletrendszer, a kéttest korrekcióval javított energiaszintek a korábbi 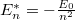\setbox0\hbox{$E_n^* = -\frac{E_0}{n^2}$}% \message{//depth:\the\dp0//}% \box0% módon számolhatók az új

\[ E_0^* = E_0 \frac{\mu}{m} = \frac{E_0}{1+\textstyle \frac{m_e}{M}} \approx E_0 \left(1- \frac{m_e}{M}\right) \]

ionizációs energiával, ahol 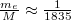\setbox0\hbox{$\frac{m_e}{M}\approx\frac{1}{1835}$}% \message{//depth:\the\dp0//}% \box0%.


A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Kvantummechanikai_bevezető_példák_-_Bohr-féle_hidrogénmodell_kéttest_korrekciója&oldid=9358”