„Kvantummechanikai bevezető példák - Izzólámpa látható tartományban kibocsátott teljesítménye” változatai közötti eltérés
A Fizipedia wikiből
a |
a (Szöveg koherenssé tétele) |
||
| 10. sor: | 10. sor: | ||
== Feladat == | == Feladat == | ||
</noinclude><wlatex># Egy izzólámpában a volfrámszál hőmérséklete kb. $1800\,\mathrm{^\circ C}$. Az emberi szem a $4-7\cdot 10^{-7}\,\mathrm{m}$ hullámhossz tartományban lát. Becsülje meg az izzólámpa „hatásfokát”! | </noinclude><wlatex># Egy izzólámpában a volfrámszál hőmérséklete kb. $1800\,\mathrm{^\circ C}$. Az emberi szem a $4-7\cdot 10^{-7}\,\mathrm{m}$ hullámhossz tartományban lát. Becsülje meg az izzólámpa „hatásfokát”! | ||
| − | </wlatex><includeonly><wlatex>{{Útmutatás|content=Használja a Planck-féle sugárzási törvényt, a látható intervallumban alkalmazzon közelítést.}}{{Végeredmény|content=$$\frac{\Delta \mathcal{E}}{\mathcal{E}_t}=0{,}355\%$$}}</wlatex></includeonly><noinclude> | + | </wlatex><includeonly><wlatex>{{Útmutatás|content=Használja a ''Planck''-féle sugárzási törvényt, a látható intervallumban alkalmazzon közelítést.}}{{Végeredmény|content=$$\frac{\Delta \mathcal{E}}{\mathcal{E}_t}=0{,}355\%$$}}</wlatex></includeonly><noinclude> |
== Megoldás == | == Megoldás == | ||
| − | <wlatex>A Planck-féle sugárzási törvény szerint a fekete test által a teljes térszögbe a $[\nu, \nu+\mathrm{d}\nu]$ frekvenciaintervallumban felületegységenként kisugárzott teljesítmény | + | <wlatex>A ''Planck''-féle sugárzási törvény szerint a fekete test által a teljes térszögbe a $[\nu, \nu+\mathrm{d}\nu]$ frekvenciaintervallumban felületegységenként kisugárzott teljesítmény |
$$ \mathcal{E}_\nu\,\mathrm{d}\nu = \frac{8\pi}{c^2} \frac{h\nu^3}{e^{\textstyle \frac{h\nu}{kT}}-1}\,\mathrm{d}\nu, $$ | $$ \mathcal{E}_\nu\,\mathrm{d}\nu = \frac{8\pi}{c^2} \frac{h\nu^3}{e^{\textstyle \frac{h\nu}{kT}}-1}\,\mathrm{d}\nu, $$ | ||
ahol bevezetjük az $x=\frac{h\nu}{kT}$ változót, és kiszámítjuk az összes kisugárzott teljesítményt: | ahol bevezetjük az $x=\frac{h\nu}{kT}$ változót, és kiszámítjuk az összes kisugárzott teljesítményt: | ||
$$ \mathcal{E}_t = \int_0^\infty \mathcal{E}_\nu \mathrm{d}\nu | $$ \mathcal{E}_t = \int_0^\infty \mathcal{E}_\nu \mathrm{d}\nu | ||
= \frac{8\pi}{c^2} \left(\frac{kT}{h}\right)^4 h \int_0^\infty \frac{x^3}{e^x-1} \,\mathrm{d}x, $$ | = \frac{8\pi}{c^2} \left(\frac{kT}{h}\right)^4 h \int_0^\infty \frac{x^3}{e^x-1} \,\mathrm{d}x, $$ | ||
| − | ahol az integrál kifejezhető a Riemann-féle $\zeta$-függvénnyel, értéke $\Gamma(4)\zeta(4)\approx 6{,}5$. | + | ahol az integrál kifejezhető a [http://mathworld.wolfram.com/RiemannZetaFunction.html ''Riemann''-féle $\zeta$-függvénnyel], értéke $\Gamma(4)\zeta(4)\approx 6{,}5$. |
A teljes térszögbe a kicsi látható $[\nu_0-\frac12\Delta\nu,\nu_0+\frac12\Delta\nu]$ tartományban felületegységenként kisugárzott teljesítményt közelíthetjük: | A teljes térszögbe a kicsi látható $[\nu_0-\frac12\Delta\nu,\nu_0+\frac12\Delta\nu]$ tartományban felületegységenként kisugárzott teljesítményt közelíthetjük: | ||
$$ \Delta \mathcal{E} = \mathcal{E}_{\nu_0} \Delta\nu, $$ | $$ \Delta \mathcal{E} = \mathcal{E}_{\nu_0} \Delta\nu, $$ | ||
| − | ahol $\nu_0=6 \cdot 10^{14}\,\mathrm{s^{-1}}$ és $\Delta \nu=4 \cdot 10^{14}\,\mathrm{s^{-1}}$ választással élünk ($\lambda_0=500\,\mathrm{nm}$ és $\Delta\lambda=375\,\mathrm{nm}$ amikor a referenciaérték intervallumközép). | + | ahol $\nu_0=6 \cdot 10^{14}\,\mathrm{s^{-1}}$ és $\Delta \nu=4 \cdot 10^{14}\,\mathrm{s^{-1}}$ választással élünk ($c=\lambda\nu$, $\lambda_0=500\,\mathrm{nm}$ és $\Delta\lambda=375\,\mathrm{nm}$ amikor a referenciaérték intervallumközép). |
Ezekkel a „hatásfok” | Ezekkel a „hatásfok” | ||
A lap 2013. május 29., 12:50-kori változata
| Navigáció Pt·1·2·3 |
|---|
| Kísérleti fizika 3. gyakorlat |
| Gyakorlatok listája: |
| Kvantummechanikai bevezető |
| Feladatok listája: |
| © 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064 |
Feladat
- Egy izzólámpában a volfrámszál hőmérséklete kb.
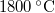. Az emberi szem a 
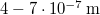hullámhossz tartományban lát. Becsülje meg az izzólámpa „hatásfokát”!
Megoldás
A Planck-féle sugárzási törvény szerint a fekete test által a teljes térszögbe a ![\setbox0\hbox{$[\nu, \nu+\mathrm{d}\nu]$}% \message{//depth:\the\dp0//}% \box0%](/images/math/f/c/9/fc93547493d2a6e8d98d5ee5959083a9.png)
frekvenciaintervallumban felületegységenként kisugárzott teljesítmény
![\[ \mathcal{E}_\nu\,\mathrm{d}\nu = \frac{8\pi}{c^2} \frac{h\nu^3}{e^{\textstyle \frac{h\nu}{kT}}-1}\,\mathrm{d}\nu, \]](/images/math/d/9/e/d9e2e1d84227762bf3e05c1837ccbb30.png)
ahol bevezetjük az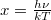 
változót, és kiszámítjuk az összes kisugárzott teljesítményt:
![\[ \mathcal{E}_t = \int_0^\infty \mathcal{E}_\nu \mathrm{d}\nu = \frac{8\pi}{c^2} \left(\frac{kT}{h}\right)^4 h \int_0^\infty \frac{x^3}{e^x-1} \,\mathrm{d}x, \]](/images/math/7/d/8/7d8a9c14625a74cc20161f2cad0234dd.png)
ahol az integrál kifejezhető a Riemann-féle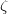 
-függvénnyel, értéke 
.
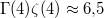A teljes térszögbe a kicsi látható ![\setbox0\hbox{$[\nu_0-\frac12\Delta\nu,\nu_0+\frac12\Delta\nu]$}% \message{//depth:\the\dp0//}% \box0%](/images/math/4/0/3/403863cf62608e4b3637ecf4549b7308.png)
tartományban felületegységenként kisugárzott teljesítményt közelíthetjük:
![\[ \Delta \mathcal{E} = \mathcal{E}_{\nu_0} \Delta\nu, \]](/images/math/7/5/6/75612cbff3866be42bf2f2145971c243.png)
ahol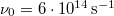 
és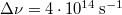 
választással élünk (
, 
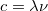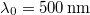és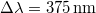 
amikor a referenciaérték intervallumközép).
Ezekkel a „hatásfok”
![\[ \frac{\Delta \mathcal{E}}{\mathcal{E}_t} = \frac{4,976 \cdot 10^{-5}\,\mathrm{\frac{W}{m^2}}}{1,400 \cdot 10^{-2}\,\mathrm{\frac{W}{m^2}}} = 3{,}55 \cdot 10^{-3} = 0{,}355\%. \]](/images/math/d/3/b/d3b1eef2a3b4b447745f38b2307e25b1.png)
