„Kvantummechanikai bevezető példák - Korrespondencia-elv a Bohr-féle hidrogénmodellben” változatai közötti eltérés

A Fizipedia wikiből
(Új oldal, tartalma: „<noinclude> Kategória:Kísérleti fizika 3. gyakorlat Kategória:Szerkesztő:Stippinger Kategória:Kvantummechanikai bevezető {{Kísérleti fizika gyakorlat …”)
 
9. sor: 9. sor:
 
}}
 
}}
 
== Feladat ==
 
== Feladat ==
−
</noinclude><wlatex># Mutassa meg, hogy miként teljesül a „korrespondencia elv” a hidrogénatom Bohr-féle modelljében a fénykibocsátása esetén!</wlatex><includeonly><wlatex>{{Útmutatás|content=$$keplet$$}}{{Végeredmény|content=$$keplet$$}}</wlatex></includeonly><noinclude>
+
</noinclude><wlatex># Mutassa meg, hogy miként teljesül a „korrespondencia-elv” a hidrogénatom Bohr-féle modelljében a fénykibocsátása esetén!</wlatex><includeonly><wlatex>{{Útmutatás|content=$$keplet$$}}{{Végeredmény|content=$$keplet$$}}</wlatex></includeonly><noinclude>
 
== Megoldás ==
 
== Megoldás ==
−
<wlatex>Megoldás szövege
+
<wlatex>A klasszikus elektrodinamika szerint a körpályán mozgó elektron által kibocsátott sugárzás körfrekvenciája éppen [[Kvantummechanikai bevezető példák - Bohr-féle hidrogénmodell|a keringés körfrekvenciája]]:
 +
$$ \omega_n = \frac{2\pi r_n}{v_n} = \frac{2\pi a_0}{v_0} \frac{1}{n^3} = \frac{m_e e^4}{4\varepsilon_0^2 h^3} \frac{1}{n^3}. $$
 +
 
 +
A Bohr-modell [[Kvantummechanikai bevezető példák - Fluxuskvantálás szemléletesen|4. posztulátuma]] szerint az energiaszintek közötti átmenetekre $\hbar \omega = E_f-E_i$, azaz
 +
$$ \hbar \omega = \frac{m_e e^4}{8\varepsilon_0^2 h^2} \left( \frac{1}{n^2} - \frac{1}{(n+1)^2} \right). $$
 +
 
 +
A korrespondencia-elv szerint a magasan gerjesztett kvantumállapotok esetén ez a kvantummechanikai kifejezés megegyezik a klasszikus elméletből származó eredménnyel. Ezt igazolja a nagy $n$-ekre
 +
$$ \frac{1}{n^2} - \frac{1}{(n+1)^2} = \frac{2n+1}{n^2(n+1)^2} \propto \frac{2}{n^3} $$
 +
kapott aszimptotikus viselkedés.
 
</wlatex>
 
</wlatex>
 
</noinclude>
 
</noinclude>

A lap 2013. április 24., 19:32-kori változata

Navigáció Pt·1·2·3
Kísérleti fizika 3. gyakorlat
Gyakorlatok listája:
  1. Kinetikus gázelmélet, transzport
  2. Állapotváltozás, I. főtétel
  3. Fajhő, Körfolyamatok
  4. Entrópia, II. főtétel
  5. Homogén rendszerek
  6. Fázisátalakulások
  7. Kvantummechanikai bevezető
Kvantummechanikai bevezető
Feladatok listája:
  1. Nap felszíni hőmérséklete
  2. Izzólámpa hatásfoka
  3. Fekete test
  4. Tantál kilépési munkája
  5. Compton-szórás
  6. Compton-szórás szabadon
  7. Fluxuskvantálás
  8. Bohr-modell
  9. Rel. tömegnövekedés
  10. Kéttest korrekció
  11. Visszalökődés
  12. Korrespondencia-elv
  13. Foton és elektron Ekin(k)
  14. Schrödinger-egyenlet
© 2012-2013 BME-TTK, TÁMOP4.1.2.A/1-11/0064

Feladat

  1. Mutassa meg, hogy miként teljesül a „korrespondencia-elv” a hidrogénatom Bohr-féle modelljében a fénykibocsátása esetén!

Megoldás

A klasszikus elektrodinamika szerint a körpályán mozgó elektron által kibocsátott sugárzás körfrekvenciája éppen a keringés körfrekvenciája:

\[ \omega_n = \frac{2\pi r_n}{v_n} = \frac{2\pi a_0}{v_0} \frac{1}{n^3} = \frac{m_e e^4}{4\varepsilon_0^2 h^3} \frac{1}{n^3}. \]

A Bohr-modell 4. posztulátuma szerint az energiaszintek közötti átmenetekre 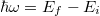\setbox0\hbox{$\hbar \omega = E_f-E_i$}% \message{//depth:\the\dp0//}% \box0%, azaz

\[ \hbar \omega = \frac{m_e e^4}{8\varepsilon_0^2 h^2} \left( \frac{1}{n^2} - \frac{1}{(n+1)^2} \right). \]

A korrespondencia-elv szerint a magasan gerjesztett kvantumállapotok esetén ez a kvantummechanikai kifejezés megegyezik a klasszikus elméletből származó eredménnyel. Ezt igazolja a nagy \setbox0\hbox{$n$}% \message{//depth:\the\dp0//}% \box0%-ekre

\[ \frac{1}{n^2} - \frac{1}{(n+1)^2} = \frac{2n+1}{n^2(n+1)^2} \propto \frac{2}{n^3} \]

kapott aszimptotikus viselkedés.

A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Kvantummechanikai_bevezető_példák_-_Korrespondencia-elv_a_Bohr-féle_hidrogénmodellben&oldid=9416”