Kísérleti fizika 3. gyakorlat: Teljes példasor
A Fizipedia wikiből
Az egyes feladatsorok a legfontosabb képletekkel kiegészítve egyenként is elérhetőek a címekre klikkelve.
Tartalomjegyzék |
Kinetikus gázelmélet, transzportfolyamatok
- Fejezze ki az egyatomos ideális gáz nyomását a gáz
belső energiájával és 
térfogatával!Végeredmény![\[p=\frac{2U}{3V}\]](/images/math/7/9/a/79a5ef5aee3e9a6d7f09326b91f3a4b4.png)
- Stern híres kísérletében, amellyel a Maxwell-eloszlás kísérleti igazolását adta,
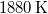-es ezüstszálról távozó atomok sebességeloszlását mérte meg, az ábrán vázolt elrendezéssel. Az 
pontbeli tengelyen elhelyezkedő szálról távozó ezüstatomok az 
nyíláson át jutottak az 
sugarú hengerfelületre. A berendezés 
szögsebességgel forgott, aminek következtében a 
sebességű atom az 
pont helyett 
-ben csapódott le.
- a) Állapítsuk meg az
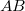ív 
hosszát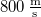 
sebességű atomok esetén, ha a fordulatszám 
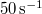és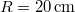 
!Végeredmény![\[x=\frac{\omega R^2}{v}\]](/images/math/0/b/6/0b64d775cd07f10acdc2f74976361052.png)
- b) Milyen sebességnél adják a legnagyobb rétegvastagságot a külső hengerfelületen lecsapódó ezüstatomok?ÚtmutatásAz időegység alatt lecsapódó részecskék számát határozzuk meg a Maxwell-eloszlás alapján, és használjuk ki az
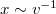összefüggést. Végeredményahol![\[v_m=\sqrt{\frac52}\,v_0,\]](/images/math/b/b/e/bbec4f31fa99ad4b348e8f27cca0b017.png)
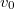a legvalószínűbb sebesség.
- a) Állapítsuk meg az
- Az
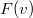sebességeloszlási függvényből a 
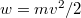összefüggés felhasználásával vezessük le az 
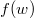energia-eloszlási függvényt, ahol 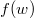azt mutatja meg, hogy az összes molekula hányadrésze rendelkezik 
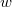és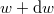 
közötti mozgási energiával! Mekkora a legvalószínűbb 
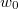energia és mennyi az átlagos kinetikus energia?Végeredmény![\[f(w)=\frac{4}{v_0\sqrt{\pi}}\frac{1}{w_v\sqrt{2\mu}}\sqrt{w} \exp\left\{ -\frac{w}{w_v} \right\}, \text{ ahol } w_v=\frac12 \mu v_0^2=kT\]](/images/math/4/6/e/46ed18cb6e204a14b7d02f1f6f168d50.png)
![\[w_0=\frac12kT,\qquad \langle w\rangle=\frac32kT\]](/images/math/3/a/7/3a7857f15c6a811008e25cebad3e2a36.png)
- Legfeljebb mekkora lehet az
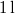térfogatú, gömb alakú edényben lévő 
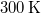-es hidrogéngáz nyomása, hogy az átlagos szabad úthossz nagyobb legyen az edény átmérőjénél? A hidrogénmolekula átmérője 
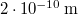.Végeredményahol![\[p<\frac{kT}{2\sqrt{2}\, R \, d^2\pi}=0{,}188\,\mathrm{Pa},\]](/images/math/f/1/3/f13f6dbd41c6c990671c0eb82ccfe194.png)
az 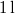-es tartály sugara.
- Hogyan változik az ideális gáz
diffúziós állandója és 
belső súrlódási együtthatója, ha a gáz térfogata -szersére nő
- a) állandó hőmérsékleten,Végeredmény -szeres, változatlan.
- b) állandó nyomáson?Végeredmény
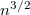-szeres, 
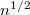-szeres.
- a) állandó hőmérsékleten,
- térfogatú, vékonyfalú tartályban ideális gáz van, az edényt légüres tér veszi körül. Feltesszük, hogy a gáz kiáramlása lassú, így a gáz egyensúlyi állapotát a folyamat nem zavarja, továbbá a lyuk mérete sokkal kisebb, mint a szabad úthossz, tehát a lyuk területére is érvényes az az összefüggés, hogy az edény falának időegység alatt nekiütköző molekulák száma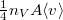
, ahol 
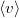a molekulák átlagsebessége. A hőmérséklet mindvégig 
.
- a) Hogyan változik az idő függvényében az edényben lévő gáz
részecskeszáma, ha a tartály falán igen kicsi, területű lyuk van?Végeredményahol![\[N(t)=n_0\exp\{-t/\tau\},\]](/images/math/0/f/6/0f66732b3648dd5d9e4a439bd08de0d9.png)
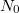a kezdeti részecskeszám-sűrűség, 
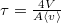. - b) Határozzuk meg azt az időtartamot, amely alatt a gáz nyomása felére csökken!Végeredmény
![\[\tau_{1/2}=\tau \ln 2\]](/images/math/8/9/8/8988e91daa948b7308b8d2c1d7b6f229.png)
- a) Hogyan változik az idő függvényében az edényben lévő gáz
- Két azonos térfogatú tartály kapcsolódik egymáshoz, a szabad úthosszhoz képest kisméretű nyíláson keresztül. Az egyikben
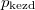nyomású, a másikban kétszer akkora nyomású hidrogéngáz van. A gázok hőmérséklete azonos és időben állandó. A kinetikus gázelmélet segítségével mutassuk ki, hogy a két tartályban azonos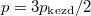 
egyensúlyi nyomás alakul ki!ÚtmutatásHasználjuk ki, hogy egyensúlyban az egyes edényekben a molekulák térfogati sűrűsége állandó, és az összes molekulák száma a folyamatban nem változik.
- Két azonos térfogatú tartály kapcsolódik egymáshoz, a szabad úthosszhoz képest kisméretű nyíláson keresztül. Az egyikben 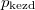nyomású hidrogéngáz, a másikban kétszer akkora nyomású oxigéngáz van. A gázok hőmérséklete azonos és időben állandó. A kinetikus gázelmélet segítségével mutassuk ki, hogy a két tartályban azonos 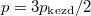egyensúlyi nyomás alakul ki!ÚtmutatásHasználjuk ki, hogy a két gáz nem hat kölcsön, alkalmazzuk a parciális nyomások tételét.
- Egy
vastagságú, nagy felületű, homogén anyagréteg két ellentétes felületén a hőmérséklet állandó 
és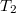 
, az anyag hővezetési tényezője hőmérséklet- és helyfüggetlen. A hővezetés alapegyenlete segítségével mutassuk ki, hogy a rétegben a hőmérséklet lineárisan változik az egyik felülettől mért 
távolsággal, és írjuk fel a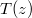 
függvényt a megadott mennyiségekkel!Végeredmény![\[T(z)=T_1+\frac{T_2-T_1}{d}z\]](/images/math/b/6/5/b6576fbfcb4cdb76f8702fbc59f78dae.png)
- Mennyi idő alatt képződik
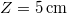vastag jégréteg egy tó felszínén, ha a léghőmérséklet 
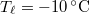, a víz hőmérséklete a jégréteg alatt 
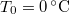? Tegyük fel, hogy a jégréteg felső felülete mindig azonos hőmérsékletű a levegővel, alső felülete pedig mindig 
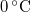-os. A jég olvadáshője 
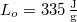, hővezetési tényezője 
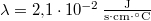, sűrűsége pedig 
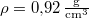.ÚtmutatásÍrjuk fel egy elemi időtartam alatt keletkező elemi vastagságú jégréteg felszabadulásakor keletkező hőt, és tegyük fel, hogy ez a jégrétegen keresztül hővezetéssel távozik, majd integráljuk a kapott egyenletet. Az analitikus megoldás érdekében hanyagoljuk el a jég fajhőjét.Végeredmény5 óra alatt képződik![\[t(Z) = \left(\frac{\rho L_o}{2\lambda(T_0-T_\ell)}\right)\,Z^2, \]](/images/math/d/8/7/d876a0a553d038419a342caf35cbffed.png)
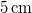vastag jégréteg.
-
hőmérsékletű, igen nagy hőkapacitású folyadékba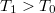 
hőmérsékletű, 
tömegű és 
fajhőjű, abszolút jó hővezető testet helyezünk a 
pillanatban. A test lehűlése a Newton-féle lehűlési törvény szerint zajlik (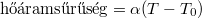
), az 
hőátadási tényező ismert, a test felületének nagysága . Határozzuk meg a test hőmérsékletét 
idő eltelte után!ÚtmutatásA leadott hőt fejezzük ki egyrészt a hőkapacitással, és a hőmérsékletváltozással, másrészt a folyadékba történő hőátadással, és integráljuk a kapott egyenletet.Végeredmény![\[T = T_0+\left(T_1-T_0\right)e^{\textstyle -\frac{A\alpha}{cm}t}\]](/images/math/1/3/f/13f20fc241d9d56f3b09002a2987438f.png)
Állapotváltozás, I. főtétel
- Készítsen vázlatos ábrát ideális gáz
- a) izochor,
- b) izobár,
- c) izoterm és
- d) adiabatikus
- állapotváltozásáról
, 
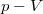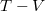és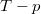 
koordináta-rendszerekben úgy, hogy a kiindulási állapot minden esetben ugyanaz legyen!
- Ábrázolja vázlatosan ideális gáz
- a) izochor,
- b) izobár,
- c) izoterm és
- d) adiabatikus
- állapotváltozásánál a belső energiának a hőmérséklettől-, térfogattól- és a nyomástól való függését! Legyen a belső energia az ordináta, és minden folyamatnál legyen ugyanaz a kiindulási állapot!
- Állapítsuk meg, milyen összefüggés van egy ideális gáz által állandó nyomáson végzett
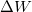munka, a gázzal közölt 
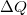hőmennyiség és a 
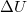belső energia-változás között, ha a 
fajhőviszony ismert!Végeredmény![\[\Delta Q = \frac{\gamma}{\gamma-1}\Delta W = \gamma \Delta U\]](/images/math/8/5/b/85be9e56262f39a875414a126cad154e.png)
- Ha egy rendszert az ábrán látható 1 úton viszünk az állapotból a állapotba,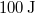
hőt vesz fel, miközben 
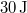munkát végez.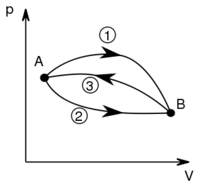
- a) Mennyi hőt vesz fel a rendszer az és állapotok közt a 2 úton, ha közben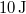
munkát végez?Végeredmény![\[\Delta Q = 80\,\rm{J}\]](/images/math/5/c/e/5ce69d1df43da9c44332675f00e619cb.png)
- b) Ha
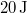munkával vihetjük a rendszert -ből -ba a 3 út mentén, mennyi a közben leadott hő?Végeredmény![\[\Delta Q = 90\,\rm{J}\]](/images/math/0/8/c/08ce50a287cbb333107df509b4469cb7.png)
- a) Mennyi hőt vesz fel a rendszer az
- Mutassa meg, hogy ideális gáz izoterm összenyomásánál a kompresszibilitás
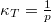, míg adiabatikus összenyomásnál 
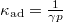, ahol 
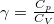.ÚtmutatásHasználjuk a kompresszibilitás definícióját, és a megfelelő folyamatokat leíró egyenleteket.Végeredmény![\[\kappa_{\mathit{ad}}=\frac{1}{\gamma p}\]](/images/math/1/f/e/1feb5ea49c75fe40f04869aa24729ef9.png)
- A
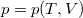állapotegyenlet ismeretében fejezzük ki a 
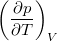mennyiséget a 
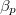hőtágulási együttható és a 
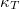izotermikus kompresszibilitás segítségével!ÚtmutatásHasználja fel a két mennyiség definícióját és azt, hogy állandó nyomáson a
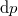teljes differenciál nulla. Végeredmény![\[{\left(\frac{\partial p}{\partial T}\right)}_V = \frac{\beta_p}{\kappa_T}\]](/images/math/e/4/9/e496792ff87f32233de1607c8704883d.png)
- Egy térfogatú szobában befűtünk. A szobában a hőmérséklet eközben állandó légköri nyomáson -ről 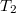-re nő. Mennyivel változik a szobában lévő levegő belső energiája?VégeredményNem változik.
- Egy kezdetben
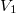térfogatú, fajhőviszonyú ideális gáz térfogatát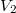 
-re növeljük. A folyamatot egyszer adiabatikusan, másodszor pedig izotermikusan hajtjuk végre. Az első és második végállapotban a nyomások aránya 
. Mekkora a 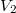térfogat?Végeredmény![\[V_2=V_1\,2\frac{1}{\gamma-1}\]](/images/math/7/d/5/7d587d64171a43d070331fc0db59c195.png)
- Van der Waals-gázok belső energiájának térfogatfüggése az alábbi összefüggéssel adható meg: ahol
![\[ U = c_V mT - \frac{m^2}{M^2}\frac{a}{V},\]](/images/math/b/4/7/b47f383e5a17bd995a4937b18f1989c8.png)
a gáz tömege, 
a móltömeg,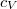 
az állandó térfogaton mért fajhő, 
állandó.
Egy hőszigetelt tartályt rögzített, jó hővezető anyagból készített fal választ két részre, amelyekbe azonos tömegű Van der Waals-gázt vezettünk be. A kezdeti állapotjellemzők: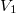, , illetve , .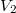
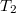- a) Mennyi lesz a végső egyensúlyi hőmérséklet?Végeredmény
![\[T=\frac{T_1+T_2}{2}\]](/images/math/4/5/d/45d22e35974fa6f3871ee196153942fb.png)
- b) Hogyan módosul a válasz, ha a gáz betöltése után az elválasztó falat rögtön kivesszük?ÚtmutatásAlkalmazzuk az I. főtételt. A gáz fajhőjét tekintsük állandónak.Végeredmény
![\[T=\frac{T_1+T_2}{2}-\frac{ma\left(V_1-V_2\right)^2}{2M^2c_VV_1V_2\left(V_1+V_2\right)}\]](/images/math/7/9/5/795c653443761983b2ab64515717f29d.png)
- a) Mennyi lesz a végső egyensúlyi hőmérséklet?
- Kondenzált (folyadék vagy szilárd) anyagok egyik közelítő állapotegyenlete Mi az
![\[V= V_0(1-ap+bT).\]](/images/math/3/2/d/32dfd83af77dc0541a76a1b499f794f8.png)
és 
paraméterek jelentése?Végeredmény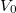
térfogatnál érvényes izotermikus kompresszibilitás és hőtágulási együttható.
- Szilárd testek hőtágulási együtthatója, illetve izotermikus kompresszibilitása alacsony hőmérsékleten az alábbi összefüggésekkel adható meg: (
![\[ \beta_p = \frac{3aT^3}{V},\qquad \kappa_T=\frac{b}{V} \]](/images/math/c/4/5/c452cee6e528e707dc57f0f8a8cb00da.png)
és állandók). Határozzuk meg a szilárd test ilyenkor érvényes állapotegyenletét!ÚtmutatásIntegráljuk a fenti mennyiségek definíciós egyenletét!Végeredményahol![\[p=\frac{3a}{4b}T^4+\frac{V_0-V}{b},\]](/images/math/f/0/3/f03818c4d7f756ea3d47cd7ddb4bed96.png)
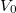állandó.
- Fejezzük ki a
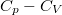különbséget mol Van der Waals-gáz esetén a hőmérséklet, a térfogat és a 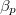hőtágulási együttható segítségével!ÚtmutatásHasználjuk fel az általánosegyenletet, a Van der Waals-gáz belső energiájára vonatkozó összefüggést és a hőtágulási együttható definícióját.![\[C_p-C_V=\frac{1}{n}\left(p+\left(\frac{\partial U}{\partial V}\right)_T\right)\left(\frac{\partial V}{\partial T}\right)_p\]](/images/math/c/3/4/c342b7595e6daf4375e0a9e1fafdf029.png)
Végeredmény![\[C_p-C_V=\frac{RT\beta_p}{1-nb/V}.\]](/images/math/a/7/4/a746f69df3bc690df6825fc3ea6c9d2d.png)
Fajhő, Körfolyamatok
- Melegszik vagy lehűl az
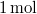ideális gáz, ha a 
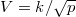összefüggés (
állandó) szerint tágul ki? Mekkora a gáz mólhője ebben a folyamatban, ha állandó térfogaton mért mólhője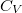 
?ÚtmutatásA fajhő általános definícióját használjuk, majd az állapotváltozás „pályáját” megadó egyenlet segítségével keressük meg a
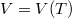függvényt és abból a 
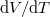hányadost! VégeredményLehűl,![\[C=C_V-R\]](/images/math/9/1/6/916d05fdbb5dfa7f9b35fed114625c98.png)
- Határozzuk meg azon lehetséges folyamatokat megadó összefüggést, amelyek közben az ideális gáz mólhője állandó (az állandó nyomáson és állandó térfogaton mért mólhőket tekintsük ismertnek)! Vezessük le a kapott egyenletből az ismert, állandó mólhőjű speciális folyamatok egyenletét.ÚtmutatásAz első főtételbe írjuk be az állandónak feltételezett mólhőt, az állapotegyenlet segítségével küszböljük ki az egyenletből a hőmérsékletet, majd oldjuk meg a
-re és -re kapott differenciálegyenletet. Végeredmény![\[pV^\frac{C-C_p}{C-C_V}=\text{állandó}.\]](/images/math/0/8/4/0844c7b8571b41dceb34b69f2c02e722.png)
- Ideális gáz állapotváltozását a 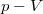síkon a
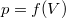összefüggés írja le.
- a) Bizonyítsa be, hogy ebben a folyamatban a fajhő térfogatfüggését a összefüggés adja meg!
![\[c(V)=c_V+R\frac{f(V)}{f(V)+V\frac{\mathrm{d}f}{\mathrm{d}V}}\]](/images/math/9/5/f/95f7a48280858181d4b28ca447b3a9d2.png)
ÚtmutatásA fejhő definíciós egyenletébe írjuk be a megadott függvényt, használjuk az állapotegyenletet és alkalmazzuk aösszefüggést!![\[\frac{\mathrm{d}V}{\mathrm{d}T}=\left(\frac{\mathrm{d}T}{\mathrm{d}V}\right)^{-1}\]](/images/math/c/8/8/c88d2444320e13642d1d1bc1085d8c92.png)
- b) Milyen
, 
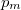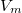értékpárnál maximális a gáz hőmérséklete, ha az állapotváltozást a 
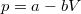egyenlet adja meg ( és ismert pozitív állandók)?ÚtmutatásHasználjuk ki, hogy a maximális hőmérsékletnek megfelelő izoterma az állapotváltozást leíró görbe érintője, ahol a fajhőnek szingularitása van!Végeredmény![\[V_m=\frac{a}{2b}\qquad\text{és}\qquad p_m=\frac{a}{2}\]](/images/math/0/4/f/04f5f3e0fd92c07431c1162d1bfa547a.png)
- a) Bizonyítsa be, hogy ebben a folyamatban a fajhő térfogatfüggését a
- Az első ábrán egy ideális gázzal végzett körfolyamat 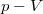diagramja látható. Ábrázoljuk a folyamatot 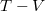és 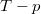diagramon!
- A második ábrán egy ideális gázzal végzett körfolyamat 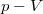diagramja látható. Mekkora a gáz által végzett munka?
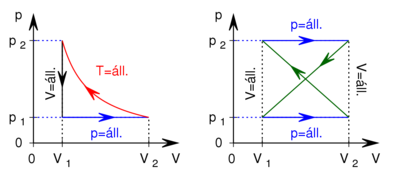Végeredmény![\[W=0.\]](/images/math/1/5/d/15d71ac95674055e4c06112ae5313e2d.png)
-
, 
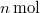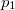nyomású kétatomos ideális gázt 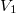térfogatról állandó nyomáson 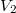térfogatúra nyomunk össze (az ábrán 1-es út). Ezen az állandó térfogaton eredeti hőmérsékletére melegítjük (2-es út), majd izotermikusan a kiinduló térfogatára tágítjuk (3-as út).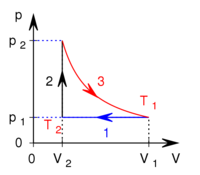
- a) Mennyivel változott a gáz belső energiája az 1-es úton?Végeredmény
![\[\Delta U_1 = p_1 \frac{V_2-V_1}{\gamma-1}, \qquad \gamma=\frac75\]](/images/math/2/f/6/2f69cad7cc3d66fb56085b61806960b8.png)
- b) Mennyivel hőt kellet közölnünk a gázzal a 2-es úton?Végeredmény
![\[\Delta Q_2=-\Delta U_1\]](/images/math/b/4/5/b45afb1d5d8899648966d216d44c756b.png)
- c) Mekkora a gáz által végzett munka és a gáz által felvett hő a teljes körfolyamatban?Végeredmény
![\[\Delta W = \Delta Q = p(V_2-V_1)+p_1V_1\ln\left(\frac{V_1}{V_2}\right)\]](/images/math/4/7/5/475bbd601cdf9182147bca5dfa9123cb.png)
- a) Mennyivel változott a gáz belső energiája az 1-es úton?
- Egy Carnot-hűtőgép egyik hőtartályában
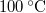hőmérsékletű, forrásban lévő víz, a másikban 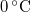hőmérsékletű víz van. A víz forráshője 
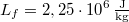, a jég olvadáshője 
.
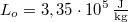- a) Mennyi vizet kell az alsó hőtartályban 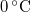hőmérsékletű jéggé fagyasztani ahhoz, hogy a felső hőtartályban
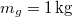tömegű 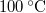hőmérsékletű gőz keletkezzék?Végeredményahol![\[m_j=(1-\eta)L_f m_g/L_o=49{,}16\,\mathrm{kg},\]](/images/math/f/1/4/f147478a59f517a1b7dfabbe7bddefd5.png)
a körfolyamat hatásfoka. - b) Mennyi külső munkát kell a körfolyamatba betáplálni?Végeredményahol
![\[W=\eta L_f m_g=6{,}03\cdot 10^5\,\mathrm{J},\]](/images/math/f/5/9/f59e5efd869a9a6687ee70f425700363.png)
a körfolyamat hatásfoka.
- a) Mennyi vizet kell az alsó hőtartályban
- Az ábrán a
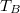és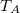 
hőmérsékletekkel meghatározott körfolyamat látható. Mekkora annak a gépnek a hatásfoka, amelyik ezt a körfolyamatot mólnyi mennyiségű, adott fajhőviszonyú ideális gázzal valósítja meg?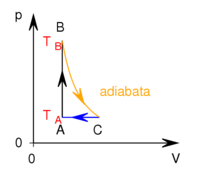
Végeredményahol![\[\eta=1-\gamma\frac{x^{1/gamma}-1}{x-1},\]](/images/math/e/e/c/eec4e9f8a52e569065ee348f1a0d0fad.png)
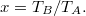
- mólnyi ideális gáz az ábrán látható körfolyamatot végzi. A körfolymat két izobár és két adiabata szakaszból áll, amelyeket a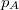
, 
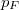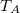, és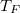 
adatok határoznak meg (ez a gőzgép sémája).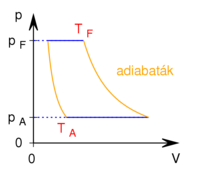
- a) Mekkora a gőzgép hatásfoka?
- b) Hogyan függ a hatásfok attól, hogy hány atomos gázmolekulákkal végezzük a körfolyamatot?
- c) Az adott gépnél és az adott gáznál hogyan növelhető a hatásfok?Végeredménya)
![\[\eta=1-\left(\frac{p_A}{p_F}\right)^{\frac{\gamma-1}{\gamma}}.\]](/images/math/b/0/6/b06b768320fb25e906c3a14c04833bbe.png)
b) A molekulák szabadsági fokának csökkentésével a hatásfok nő.
c) A nyomásviszony növelésévekl a hatásfok nő.
- Egy épület fűtésére az ún. dinamikus fűtést használjuk:
- A fűtőanyagot elégetjük egy hőerőgép tűzszekrényében, melynek hőmérsékletét állandó hőmérsékleten tartjuk (ez a hőerőgép felső hőtartálya).
- A hőerőgép egy hőszivattyút működtet, amelynek alsó hőtartálya egy tó 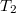hőmérsékletű vize, felső hőtartálya pedig a hőerőgépet hűtő hőmérsékletű víz, amely az épületet egyúttal fűti (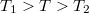
).
- A tűzszekrényben
égéshőjű anyag ég, a hőerőgép és a hőszivattyú veszteség nélkül, Carnot-hatásfokkal működik. Határozzuk meg, mennyi hőt kap a helyiség egységnyi tömegű fűtőanyag elégetése árán!Végeredmény![\[Q=q\frac{1-T_2/T_1}{1-T_2/T}>q.\]](/images/math/0/9/7/097b137e36faa49bbb8b3a3deaab5f04.png)
- A fűtőanyagot elégetjük egy hőerőgép tűzszekrényében, melynek hőmérsékletét állandó
Entrópia, II. főtétel
-
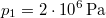nyomású, 
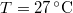hőmérsékletű és 
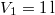térfogatú ideális gáz izotermikusan 
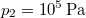nyomásig terjed ki. Mennyivel változott meg eközben az entrópiája? ÚtmutatásHasználjuk az entrópiaváltozás definícióját és az állapotegyenletet!Végeredmény![\[\Delta S=\frac{p_1 V_1}{T}\ln\frac{p_1}{p_2}=19{,}97\,\mathrm{\frac{J}{K}}\]](/images/math/6/d/0/6d0b864aa264a9c16325151512c98203.png)
- Mennyivel változik meg
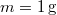nitrogéngáz entrópiája, ha állandó nyomáson 
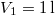térfogatról 
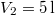térfogatra expandáltatjuk.Végeredmény![\[\Delta S=\frac{m}{\mu_\mathrm{N_2}}C_p\ln\frac{V_2}{V_1}=3{,}34\,\mathrm{\frac{J}{K}}, \qquad C_p=\frac72R.\]](/images/math/6/9/3/69379145baf5ca7bc790fdc4464b8173.png)
- Tekintsünk tömegű, móltömegű, fajhőviszonyú ideális gázt.
- a) Vezesse le az entrópia hőmérséklet- és térfogatfüggését megadó összefüggést!ÚtmutatásVizsgálja az entrópiaváltozást adiabatikus folyamatban!Végeredmény
![\[S=\frac{m}{M}R\ln\left(T^{\frac{1}{\gamma-1}}V\right)+S_0\]](/images/math/7/0/3/703497cb4e3daf33126d8a9df9ebb08d.png)
- b) A kapott entrópia-kifejezés segítségével vezesse le az adiabata egyenletét!ÚtmutatásVizsgálja az entrópiaváltozást adiabatikus folyamatban!Végeredmény
![\[TV^{\gamma-1}=\mathrm{const.}\]](/images/math/7/5/4/754140f6a21d584b63f5d26d9a18a297.png)
- a) Vezesse le az entrópia hőmérséklet- és térfogatfüggését megadó összefüggést!
- Az ideális gáz entrópiáját gyakran az
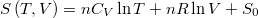alakban használják.
- a) Indokolja meg, hogy az
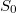mennyiségnek függnie kell a rendszer anyagmennyiségét megadó mólszámtól!VégeredményAz entrópia extenzív állapotjelző. - b) Adjon meg egy olyan
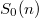-függést, amellyel az entrópia fenti kifejezése teljesíti az a) pontban szereplő követelményt!Végeredményamivel az entrópia![\[S_0(n)=-nR\ln n+ns_0,\]](/images/math/0/f/5/0f5e8e66063357f77affc5dd75e82760.png)
ahol![\[S\left(T,V\right)=n C_V\ln T+nR\ln \frac{V}{n}+ ns_0,\]](/images/math/e/5/8/e580690ef414387f9272cc6ffe11e430.png)
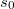már -től független.
- a) Indokolja meg, hogy az
-
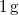
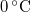-os víz állandó nyomáson 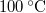-os gőzzé alakul. Határozzuk meg a folyamat alatt bekövetkező entrópiaváltozást!.Végeredmény![\[\Delta S = mc\ln\frac{373}{273}+\frac{mL_f}{373\,\mathrm{K}}=7{,}36\,\mathrm{\frac{J}{K}},\]](/images/math/8/f/f/8ff47ef68c48ff988ac413b430356235.png)
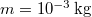a víz tömege, a víz fajhője, 
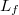a forráshője.
-
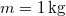tömegű, 
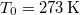hőmérsékletű vizet termikus kapcsolatba hozunk egy 
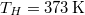hőmérsékletű hőtartállyal.
- a) Mekkora a víz entrópia-változása, miután a hőmérséklete elérte a hőtartály hőmérsékletét?Végeredmény
![\[1306\,\mathrm{\frac{J}{K}}\]](/images/math/2/d/8/2d8871a7637fa7346587bd1eb82a4c69.png)
- b) Mekkora eközben a hőtartály entrópia-változása?Végeredmény
![\[-1121\,\mathrm{\frac{J}{K}}\]](/images/math/0/3/9/039511937396c1ce27cf7b567a919c69.png)
- c) Mekkora a teljes rendszerben (hőtartály és víz) létrejött entrópia-változás?Végeredmény
![\[185\,\mathrm{\frac{J}{K}}\]](/images/math/0/6/1/06120b7dea96d50e3214e101a83a9563.png)
- d) Mennyi a teljes rendszerben létrejött entrópia-változás, ha a testet először egy
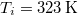hőmérsékletű hőtartállyal, majd az egyensúly beállta után a 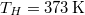hőmérsékletű hőtartállyal hozzuk kapcsolatba?Végeredmény![\[98\,\mathrm{\frac{J}{K}}\]](/images/math/9/2/9/929c0bc6fa4c0264edcf460bb60e5c28.png)
- e) Lehet-e úgy melegíteni a vizet, hogy a teljes rendszer entrópia-változása kisebb legyen egy előírt értéknél (vagyis a folyamat előírt mértékben megközelítse a reverzíbilis folyamatot)?VégeredményIgen.
- a) Mekkora a víz entrópia-változása, miután a hőmérséklete elérte a hőtartály hőmérsékletét?
- Tekintsünk ideális gázzal végzett Carnot-körfolyamatot.
- a) Ábrázoljuk a Carnot-körfolyamatot
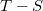diagramban!
- b) Mutassuk ki, hogy a körfolyamatban a gáz által végzett munka most is a körfolyamat területével egyenlő!
- c) Számítsuk ki a fentiek alapján a Carnot-körfolyamat hatásfokát!
- a) Ábrázoljuk a Carnot-körfolyamatot
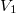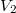- Egymástól válaszfallal elzárt, és térfogatú két edényben azonos hőmérsékletű, azonos nyomású,
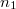és 
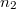mólszámú, különböző fajtájú ideális gáz van. Ha a válaszfalat eltávolítjuk, akkor a két gáz összekeveredik.
- a) Indokoljuk meg, hogy a folyamatban miért nem változik a hőmérséklet és a nyomás!VégeredményIdeális gázról van szó és érvényes a Dalton-törvény.
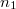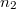- b) Határozzuk meg az entrópia-változást (az ún. keverési entrópiát), és fejezzük ki a gázok és mólszámaival!ÚtmutatásAlkalmazzuk az Ideális gáz entrópiájáról szóló feladatban kapott entrópia-kifejezést, tegyük fel, hogy a teljes edényt kitöltő két gáz mindegyikének entrópiája úgy számítható, mintha a másik nem lenne jelen, és használjuk fel a Dalton-törvényt.Végeredmény
![\[\Delta S = R n_1 \ln\frac{n_1+n_1}{n_1} + R n_2 \ln\frac{n_1+n_2}{n_2}\]](/images/math/5/9/6/596d530da1c94e91161150cb929bb191.png)
- c) Számítsuk ki az entrópia-változást, ha a két edényben azonos fajtájú gáz van!ÚtmutatásA levezetésnél vegyük figyelembe, hogy a keverés utáni állapotban az egész edényben ugyanaz a gáz van. A különböző gázokra levezetett fenti összefüggésből nem kapunk helyes eredményt; ez a Gibbs-féle paradoxon.Végeredmény
![\[\Delta S=0\]](/images/math/8/1/c/81ca578b10374e17bce8368f5500ff49.png)
- a) Indokoljuk meg, hogy a folyamatban miért nem változik a hőmérséklet és a nyomás!
-
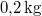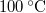, hőmérsékletű vasat hőszigetelt kaloriméterben lévő, 
, 
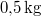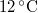-os vízbe teszünk. A vas fajhője 
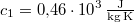, a vízé 
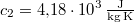. Mennyi az entrópiaváltozás a hőmérséklet kiegyenlítődése miatt, ha a nyomás állandó?Végeredmény![\[T_k=288{,}7\,\mathrm{K},\qquad \Delta S=3{,}41\,\mathrm{\frac{J}{K}}\]](/images/math/b/d/b/bdb4a99b8fe7577d94178ef75c691ba3.png)
- Két test azonos
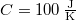hőkapacitású, de hőmérsékletük különböző: 
, 
.
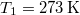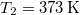- a) Mennyi lesz a közös hőmérsékletük, ha termikus kapcsolatba hozzuk őket úgy, hogy a környezet felé ne legyen hőátadás?Végeredmény
![\[T_k=\frac{T_1+T_2}{2}\]](/images/math/e/4/0/e40444a3f717bb0150a6cddb411c076d.png)
- b) Mennyi lesz a közös hőmérséklet, ha a kiegyenlítődést egy reverzíbilisen működő hőerőgép végzi?Végeredmény
![\[T_k=\sqrt{T_1 T_2}\]](/images/math/2/2/5/22549fc9b794cce58ca4c0f18c2725c4.png)
- c) Ha a kiegyenlítődés nem jár térfogatváltozással, mekkora lesz a két esetben a belső energia megváltozása és az entrópia-változás?Végeredmény
![\[\Delta U_a=0, \qquad \Delta U_b=2C\sqrt{T_1 T_2}-CT_1-CT_2=-778{,}7\,\mathrm{J},\]](/images/math/4/4/a/44a431f68a2caaec70e8da0364f277ff.png)
![\[\Delta S_a=2C\ln\frac{T_1+T_2}{2}-C\ln T_1-C\ln T_2=2{,}42\,\mathrm{\frac{J}{K}}, \qquad \Delta S_b=0.\]](/images/math/7/a/1/7a11e8b14bc0459f04ada0abf724dd1b.png)
- a) Mennyi lesz a közös hőmérsékletük, ha termikus kapcsolatba hozzuk őket úgy, hogy a környezet felé ne legyen hőátadás?
Homogén rendszerek
- Bizonyítsuk be a
, 
, 
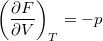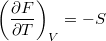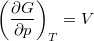és 
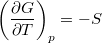összefüggéseket!
- Bizonyítsuk be a
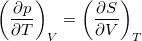Maxwell-összefüggést!
- Állandó anyagmennyiségű homogén rendszerben termikus és mechanikai kölcsönhatás esetén fennáll a
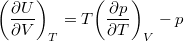egyenlet. A fenti egyenlet levezetésének mintájára bizonyítsuk be, hogy ha a termikus kölcsönhatás mellett tetszőleges – 
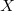intenzív- és 
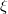extenzív mennyiségpárral jellemzett – kölcsönhatás lép fel, akkor a fenti egyenlet érvényes marad, ha végrehajtjuk a 
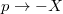és a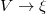 
változócserét!
- Fejezzük ki mérhető mennyiségekkel (hőtágulási együttható, kompresszibilitás, mólhő) egy rendszer
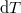hőmérséklet-változását, ha térfogata adiabatikus, kvázisztatikus folyamat során 
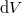-vel megváltozik! Mutassuk meg, hogy 
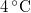alatt a víz adiabatikus, kvázisztatikus összenyomáskor lehűl!ÚtmutatásÍrjuk fel az első főtételt, írjuk be az
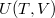függvény teljes differenciálját, alkalmazzuk a belső energia térfogatfüggésére érvényes összefüggést, és a nyomás hőmérsékletfüggéséről szóló feladat eredményét! A víz hőtágulási együtthatója 
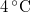alatt negatív.
- Feltételezve, hogy
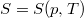, mutassuk ki, hogy 
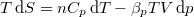, ahol 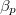az izobár hőtágulási együttható.ÚtmutatásÍrjuk fel
teljes differenciálját, használjuk a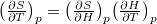 
matematikai összefüggést, a termodinamika két differenciális összefüggését és a 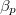definícióját.
- Az első főtétel és a termodinamika differenciálegyenletei felhasználásával mutassuk meg, hogy ha ismerjük egy állandó anyagmennyiségű rendszer belső energiáját a térfogat és az entrópia függvényeként (vagyis az
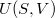függvényt), akkor a rendszer bármely állapotjelzője (nyomás, hőmérséklet, entalpia, stb.) megadható és függvényeként!
- Mennyivel változik egy tömegű, hőmérsékletű, térfogatú rendszer entrópiája, ha térfogata állandó nyomáson 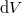értékkel megnő? Az állandó nyomáson mért
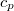fajhőt és a 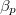hőtágulási együtthatót ismertnek tekintjük.ÚtmutatásÍrjuk fel az 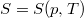függvény teljes differenciálját állandó nyomáson, és alkalmazzuk 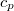és 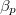definícióját! Végeredmény![\[\mathrm{d}S=\frac{m c_p}{TV\beta_p}\,\mathrm{d}V\]](/images/math/8/9/1/8913482ffd0e5fd05a97ff4d3c990a0a.png)
- Egy rendszer állapotegyenlete
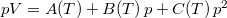, ahol a hőmérsékletfüggő együtthatók kísérletekből ismertek. Mennyit változik a rendszer szabad entalpiája és entrópiája, ha a nyomást rögzített hőmérsékleten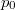 
-ról 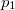-re változtatjuk?ÚtmutatásHasználjuk ki a
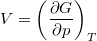és az 
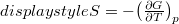összefüggéseket! Végeredményés![\[\Delta G=A\ln\left(\frac{p_1}{p_0}\right)+B\left(p_1-p_0\right)+C\frac{p_1^2-p_0^2}{2}\]](/images/math/6/0/4/604b4690f62d9f0616982b2cd9d8dfe5.png)
ahol a vessző a hőmérséklet szerinti deriváltat jelenti.![\[\Delta S=A'\ln\left(\frac{p_1}{p_0}\right)+B'\left(p_1-p_0\right)+C'\frac{p_1^2-p_0^2}{2},\]](/images/math/9/4/d/94dc473377e76fb6ed5fbb18beabd15f.png)
- Egy gumiszalag állapotegyenlete
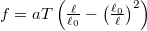alakba írható, ahol 
a szalagban fellépő húzóerő nagysága,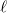 
a szalag hossza, a hőmérséklet, 
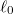a szalag erőmentes hossza, pozitív állandó.
- a) Mutassuk ki, hogy a belső energia nem függ a szalag hosszától!ÚtmutatásA belső energia térfogatfüggésére kapott általános összefüggés átírható a vizsgált esetre a
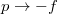és 
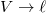helyettesítéssel. - b) Írjuk fel a termodinamika fundamentális egyenletét, továbbá a szabad energia és a szabad entalpia megváltozását a gumiszalagra!ÚtmutatásAlkalmazzuk az a) pontban leírt fenti változócseréket!Végeredmény
![\[\mathrm{d}U=T\mathrm{d}S+f\mathrm{d}\ell\]](/images/math/7/f/5/7f5decf22c82e848373c1a93e96bafaf.png)
- c) Mekkora munkát végzünk, és mennyi a gumiszalag által leadott hő, ha a szalag hosszát izotermikus, reverzíbilis folyamatban 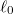-ról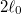
-ra növeljük.ÚtmutatásHasználjuk az I. főtételt, és vegyük figyelembe az a) részfeladat eredményét!Végeredmény![\[W=Q_\text{le}=\int_{\ell_0}^{2\ell_0}f\mathrm{d}\ell\]](/images/math/a/9/2/a92623436a83ffbf664f8f1a1b3458ef.png)
- d) Igazoljuk, hogy a gumiszalag hőmérséklete megnő, ha adiabatikusan megnyújtjuk!ÚtmutatásHasonlítsuk össze a fundamentális egyenletet és az
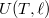függvény teljes differenciálját, és vegyük figyelembe az (a) részfeladat eredményét! Végeredményahol![\[\left(\frac{\partial T}{\partial \ell}\right)_S=\frac{f}{C_\ell}>0,\]](/images/math/4/8/f/48fb10b34970193d78d5a4a66ee9c31c.png)
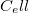az állandó hossznál mért hőkapacitás.
- a) Mutassuk ki, hogy a belső energia nem függ a szalag hosszától!
- Mennyi hő szabadul fel az
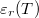dielektromos állandójú dielektrikum polarizációjakor, ha a külső elektromos tér nagyságát állandó hőmérsékleten, kvázi-stacionáriusan növeljük nulláról egy nem túl nagy 
értékre? A térfogatváltozás elhanyagolható.ÚtmutatásHasználjuk az I. főtétel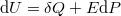
alakját, az 
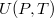függvény teljes differenciálját, és azt, hogy a belső energia térfogatfüggésére kapott általános összefüggés átírható erre az esetre is a dielektrikum teljes dipólusmomentuma (
) segítségével a 
és 
helyettesítéssel: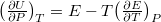 
. Alkalmazzuk még a 
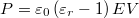összefüggést is! Végeredmény![\[Q=-\frac12T\varepsilon_0V\frac{\mathrm{d}\varepsilon_r(T)}{\mathrm{d}T}E^2\]](/images/math/7/4/8/748a2556baf501bef94eaf7c54b03a77.png)
Fázisátalakulások
- Mutassuk meg, hogy mechanikai- és termikus kölcsönhatásban részt vevő rendszerben állandó nyomáson végbemenő fázisátalakulásnál az átalakulási hő (
) az entalpiaváltozással (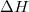
) egyenlő!ÚtmutatásHasználjuk az entalpia definícióját és az első főtételt!
-
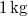víznek normál nyomáson (
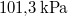) való elforralásához egy elektromos merülőforralón a 
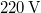-os feszültségforrásból 
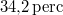-en át 
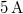áramot kell átfolyatni. A gázállandó 
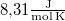, a víz moláris tömege 
.
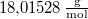Határozzuk meg a víz- a) entalpia-,Útmutatáshasználjuk fel az előző feladat eredményét az izobár átalakulási hőre.Végeredmény
![\[\Delta H = W_\text{el} = 2{,}26\,\mathrm{MJ}\]](/images/math/4/f/d/4fdaf5770143071de6a318dd403592b3.png)
- b) entrópia- ésÚtmutatáshasználjuk az entrópia definíciójátVégeredmény
![\[\Delta S = 6{,}06\,\mathrm{\frac{kJ}{K}}\]](/images/math/7/2/7/7276d2981b6be7939e2cbb7053cfb7e9.png)
- c) belső energiaváltozását ebben a folyamatban!Útmutatásírjuk fel az entalpiaváltozás és belső energiaváltozás összefüggését, hanyagoljuk el a víz térfogatát a gőzéhez képest, és a gőzt tekintsük ideális gáznak.Végeredmény
![\[\Delta U=\Delta H-\frac{m}{M}RT=2{,}09\,\mathrm{MJ}\]](/images/math/0/8/9/089fe9b22dd39aba913ca295f3f5cd56.png)
- a) entalpia-,
- Henger alakú edényben
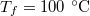hőmérsékletű telített vízgőz van. Egy súlytalan dugattyú lassú betolásának hatására az edényben 
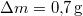víz lecsapódik. A víz moláris tömege 
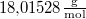A folyamat során a nyomás a 
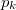külső légnyomással egyenlő.
Mennyi munkát végeztünk ezalatt az ideális gáznak tekinthető vízgőzön?Végeredmény![\[\Delta W=p_k\left(V_1-V_2\right)=\frac{RT_f}{M}\Delta m=120\,\mathrm{J}\]](/images/math/0/1/c/01c0c0abb9f739cbff493a96bc03ec39.png)
- Ábrázoljuk (kvalitatív módon) egy tiszta anyag kémiai potenciáljának
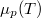hőmérsékletfüggését állandó nyomáson, az anyag szilárd-, folyadék- és gőzállapotát átfogó hőmérséklet-intervallumban! Az olvadáspontot 
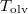-val, a forráspontot 
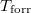-ral jelöljük, és tegyük fel, hogy a mólentrópia egy fázison belül nem függ a hőmérséklettől!ÚtmutatásHasználjuk fel aegyenletet, a kémiai potenciál és a szabad entalpia összefüggését, továbbá két fázis egyensúlyának feltételét.![\[\left(\frac{\partial G}{\partial T}\right)_p=-S\]](/images/math/5/d/3/5d3e0ea157a966637bfd4bc7513fc8bd.png)
- Felhasználva, hogy az olvadáspont az állandó nyomáson felvett
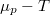diagramban a szilárd fázisra és a folyadékra érvényes görbék metszéspontjánál van mutassuk ki, hogy a nyomás növelésekor az olvadáspont nő, ha a szilárd fázis móltérfogata kisebb, mint a folyadéké! Hogyan változik a jég olvadáspontja, a nyomás növelésekor?ÚtmutatásA nyomásváltozás a 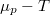görbét eltolja, mégpedig a két fázisban általában különbözőképpen. A görbe eltolódásának mértékét adott hőmérsékleten, adott fázisban a összefüggés adja meg.![\[\left(\frac{\partial \mu }{\partial p}\right)_T= V_M\]](/images/math/2/5/a/25a4030c915d37e859e677c758ddfc3f.png)
- A szilárd-folyadék egyensúlyi görbének (olvadási görbe) közelítő meghatározására gyakran használják a
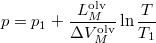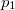összefüggést ( a nyomáson, a nyomáson érvényes olvadáspont, az egyenletben szereplő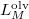 
az anyag moláris átalakulási hője (vagy moláris entalpiaváltozása), 
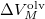pedig a móltérfogat változása az olvadásnál).
- a) Vezessük le ezt az egyenletet, és állapítsuk meg, hogy milyen feltételek mellett érvényes!ÚtmutatásIntegráljuk a Clausius-Clapeyron-egyenletet!
- b) Mutassuk ki, hogy a -hez képest kis
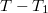érték eseten az egyensúlyi nyomás lineárisan változik a 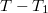különbséggel!ÚtmutatásHasználjuk fel a kis-ekre érvényes 
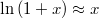összefüggést.
- a) Vezessük le ezt az egyenletet, és állapítsuk meg, hogy milyen feltételek mellett érvényes!
- A jég olvadáshője
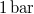nyomáson 
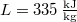. A jég és a víz fajlagos térfogatának aránya 
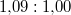. Becsüljük meg, mennyivel tolódik el az olvadáspont kis nyomásnövekedés hatására!Végeredmény![\[\mathrm{d}T=-\frac{0{,}09v_\text{víz}T}{L}\,\mathrm{d}p= -7{,}34\cdot10^{-8}\mathrm{\frac{K}{Pa}}\,\mathrm{d}p\]](/images/math/2/b/7/2b73b88d36a28976c45ec8366c83d6ee.png)
- Ha a nyomást
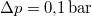-ral megnöveljük, akkor a víz forrási hőmérséklete 
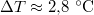-kal növekszik. Ennek felhasználásával becsüljük meg a víz forráshőjét!ÚtmutatásA vízgőzre alkalmazzuk az ideális gáz egyenletét, és hanyagoljuk el a víz fajlagos térfogatát a gőzéhez képest!Végeredmény![\[L_f\approx \frac{\Delta p}{\Delta T}\frac{RT^2}{p_kM}=2253\,\mathrm{\frac{kJ}{kg}}\]](/images/math/4/c/7/4c7c0dfc446c66a05097776d64fc920c.png)
- A szilárd argon
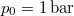nyomáson 
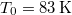hőmérsékleten olvad meg. Olvadáshője ekkor 
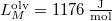, móltérfogatának változása 
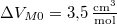. A nyomás növekedésekor kísérleti eredmények szerint az olvadáshő nem változik, a 
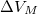móltérfogatváltozás viszont az abszolút hőmérséklet megközelítőleg 
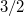-ik hatványával arányos.
Mekkora nyomást kell alkalmaznunk ahhoz, hogy az olvadási hőmérséklet megkétszereződjék?ÚtmutatásA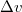
hőmérsékletfüggésének figyelembevételével integráljuk a Clausius-Clapeyron-egyenletet! Végeredmény![\[p=p_0+\frac{2L}{3\Delta v_0}\left(1-\left(\frac{T_0}{T}\right)^{3/2}\right)=1449\,\mathrm{bar}\]](/images/math/b/5/9/b59affbd1e174e38c0177e77ed696768.png)
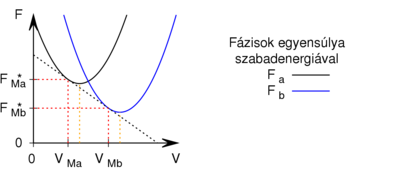
- Egy homogén anyag adott hőmérsékleten két fázisban ( és ) létezhet. Az egyes fázisok moláris szabad energiáinak térfogattól való függése (rögzített hőmérsékleten, állandó anyagmennyiség esetén) az ábrán látható.
Mutassuk ki, hogy egyensúlyi állapotban a fázisok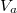
és 
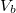térfogatai a két görbéhez húzott közös érintő érintési pontjainak abszcisszái, a közös nyomás pedig az érintő negatív iránytangense!
Útmutatásfejezzük ki a nyomást és a kémiai potenciált a szabad energiával (
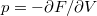, ill. 
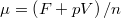), és használjuk ki, hogy fázisegyensúlyban a két fázis nyomása és kémiai potenciálja egyenlő!
- Az ábrán különböző mennyiségek hőmérsékletfüggését mutatjuk be a
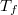fázisátalakulási hőmérséklet környezetében. Az ábrák közül melyik tartozhat elsőrendű és melyik másodrendű fázisátalakuláshoz?
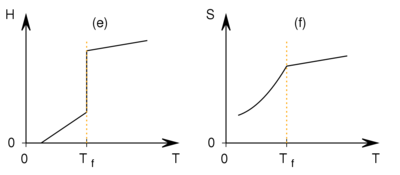
VégeredményElsőrendűek: a), b), e), h).
Másodrendűek: c)', d)', f), g).
Kvantummechanikai bevezető
- Nyári napsütésben, délben a Föld felszínének
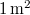-én átlagosan kb. 
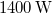napsugárzási teljesítmény mérhető. Becsüljük meg a Nap felszínének hőmérsékletét!
(
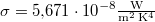)ÚtmutatásHasználjuk ki, hogy a Nap által kibocsátott összes sugárzási teljesítmény egyenletesen oszlik el egy földpálya sugarú gömbfelületen.Végeredmény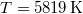
- Egy izzólámpában a volfrámszál hőmérséklete kb.
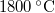. Az emberi szem a 
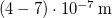hullámhossz tartományban lát. Becsülje meg az izzólámpa „hatásfokát”!ÚtmutatásHasználja a Planck-féle sugárzási törvényt, a látható intervallumban alkalmazzon közelítést.Végeredmény![\[\frac{\Delta \mathcal{E}}{\mathcal{E}_t}=0{,}355\%\]](/images/math/e/a/1/ea1bc4434817421fb132a20eb6e23fd8.png)
- Határozzuk meg, hogy egy hőmérséklet fekete test milyen foton-áramsűrűséggel sugároz!ÚtmutatásA Planck-féle sugárzási törvényben különítse el a foton energiáját.Végeredmény
![\[N = 2{,}404 \frac{8\pi}{c^2}\left(\frac{kT}{h}\right)^3\]](/images/math/5/2/5/525d3b6c79fc0b7e9c3c5bc6bbcf4e34.png)
- Egy
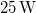-os megfelelő gázzal töltött lámpától 
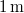-re egy tantál fémfelületet (
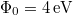) helyezünk el. A klasszikus elmélet alapján becsülje meg, hogy egy elektron átlagosan mennyi idő alatt gyűjtene össze annyi energiát, amivel kiléphet a fémből!
(A valóságban a fotoeffektus során az elektronok a megvilágításkor „azonnal” kilépnek a fémből.)ÚtmutatásHasználja fel, hogy az izzó által kibocsátott összes sugárzási teljesítmény egyenletesen oszlik el az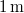 sugarú gömbfelületen. Végeredmény![\[\Delta t= \frac{16\Phi_0}{P} \left( \frac{\ell}{D_\mathrm{Ta}} \right)^2 = 4{,}88\,\mathrm{s}\]](/images/math/a/9/0/a90e4994c9b40edbfb9deab6614d74db.png)
- Határozza meg, hogy a Compton-szórás esetén a beeső foton energiájának hány százalékát adja le az elektronnak!ÚtmutatásA Compton-szórás levezetéséhez írja fel a relativisztikus energia- és impulzusmegmaradást.Végeredményahol
![\[\eta = 1 - \left(\frac{p_f(1-\cos\vartheta)}{m_e c}+1\right)^{-1},\]](/images/math/e/3/d/e3d6a9c5338b3763b4cad5550a858ae6.png)
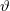a foton eltérülése eredeti irányától.
- Vizsgáljuk meg, hogy létezik-e olyan effektus, hogy egy szabad elektron teljes egészében elnyel egy fotont (teljesen rugalmatlan ütközés)! Ennek fényében, hogyan magyarázható a fotoeffektus?ÚtmutatásVizsgálja meg milyen körülmények között jöhetne létre Compton-szórás szabad elektronra.VégeredménySzabad elektronra nem létezik. Fotoeffektusnál az energiamegmaradásban figyelembe kell venni a kilépési munkát.
- Alkalmazza a Bohr–Sommerfeld-féle kvantálási hipotézist körpályán mozgó elektronra és egy lineáris oszcillátorra! Magyarázza meg a szupravezetésnél fellépő „fluxuskvantálás” jelenségét a Bohr–Sommerfeld-féle kvantálási hipotézis segítségével!ÚtmutatásÍrja fel és „kvantálja” a fázistérbeli pályaintegrált!VégeredményKörpályán mozgó elektronra
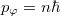, lineáris oszcillátorra 
.
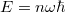- Számítsa ki a hidrogénatom Bohr-féle modelljében a „körpályán” keringő elektron pályasugarát, sebességét, perdületét és energiáját!ÚtmutatásÍrja fel a körpályán tartó Coulomb-erőt és alkalmazza a kvantumhipotézist!Végeredmény
![\[ v_n = \frac{v_0}{n}, \qquad r_n = a_0 n^2,\]](/images/math/b/e/f/befdf1be2cd0570bc1714f3c8617241f.png)
ahol![\[L_n = n\hbar, \qquad E_n = -\frac{E_0}{n^2}, \]](/images/math/f/b/6/fb6b76901bce25c085edd4b2973f8e77.png)
![\[v_0 = \frac{e^2}{4\pi\varepsilon_0\hbar}, \qquad a_0 = \frac{\hbar^2 4 \pi \varepsilon_0}{m_e e^2}, \]](/images/math/4/9/9/4999909021a110d647609282a1008127.png)
![\[ E_0 = \frac{m_e e^4}{2\hbar^2(4\pi\varepsilon_0)^2}.\]](/images/math/e/3/2/e3286e30266aeb2eb0d27f902ea46e8c.png)
- Számítsa ki, hogy a hidrogénatom Bohr-féle modelljében a relativisztikus tömegnövekedés milyen korrekciót jelentene az energiaszintekben!ÚtmutatásFejtse sorba a relativisztikus tömeget.Végeredmény
![\[ E_n = -\frac{E_0}{n^2}-\frac{E_0}{2} \frac{\alpha_f^2}{n^4}+O\left[n^{-6}\right], \]](/images/math/1/9/9/199cedfdb000e94b97da397355f62e91.png)
-ben negyedrendű korrekciót kapunk. Megjegyzendő, hogy az együttható nem pontos, mert a klasszikus relativisztikus tárgyalás nem juthat el arra a helyes eredményre, ami a kvantummechanikában a Klein–Gordon-formula néven ismert.
- Számítsa ki, hogy a hidrogénatom Bohr-féle modelljében a mag véges nagyságú tömege milyen korrekciót jelentene az energiaszintekben és a spektrumban!ÚtmutatásOldja meg a Bohr-modellt tömegközépponti koordináta-rendszerben.Végeredmény
![\[E_n^* = -\frac{E_0}{n^2},\]](/images/math/6/e/e/6ee9b65a150eb583861a491351b3a4f1.png)
ahol![\[ E_0^* = \frac{E_0}{1+\textstyle \frac{m_e}{M}} \approx E_0 \left(1- \frac{m_e}{M}\right), \]](/images/math/3/c/f/3cfa608d96f63f174a55fb8b88a36a1c.png)
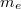az elektron, pedig az atommag tömege.
- Határozza meg, hogy az atomok fotonkibocsátásakor fellépő visszalökődés milyen korrekciót jelent az emissziós spektrumban!ÚtmutatásAlkalmazza az energia- és az impulzusmegmaradás tételét.VégeredményAz új frekvenciaahol
![\[\nu' \approx \frac{\nu}{1+\displaystyle \frac{h\nu}{Mc^2}},\]](/images/math/b/3/4/b3456225f815bfd0b26120dce20131a2.png)
a visszalökődés nélküli foton frekvenciája, az atom tömege.
- Mutassa meg, hogy miként teljesül a „korrespondencia-elv” a hidrogénatom Bohr-féle modelljében a fénykibocsátása esetén!ÚtmutatásVizsgálja a hidrogénatom magasan gerjesztett állapotai közti átmeneteket.
- Hasonlítsa össze a foton és az elektron kinetikus energia-hullámszám görbéjét! Elemezze a lehetséges jellegzetességeket relativisztikus, és nemrelativisztikus esetekben!ÚtmutatásA relativisztikus összenergia
.
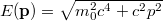- Határozza meg a Schrödinger-féle hidrogénatomban az elektron alapállapoti hullámfüggvényét! Számítsa ki, hogy protontól milyen távolságban található meg az elektron a legnagyobb valószínűséggel!ÚtmutatásAz elektron sugárirányú megtalálási valószínűségének eloszlás
![\[ R(r) = A_n \left(\frac{r}{a_0}\right)^{n-1} e^{\textstyle -\frac{r}{n a_0}}.\]](/images/math/c/0/f/c0f960f3b75cc266fda2e137a4acc04b.png)
Végeredmény![\[r_\text{lv.}=n^2 a_0\]](/images/math/b/a/7/ba7a51917aa422072b054ff3f54a2da0.png)
